Epidemije poštuju matematička pravila te su brojni matematičari i stručnjaci za podatke širom sveta svojim modelima pokazivali prilično tačne projekcije toka i kraja epidemije. Profesor Petar Kočović napravio je model koji nam tumači tok epidemije u Srbiji, pravi poređenja sa drugim zemljama u svetu i predviđa kada bismo mogli da očekujemo potpuno stišavanje zaraze.
Epidemija u Srbiji, pod uslovom da trendovi budu kao u prethodnih desetak dana, trebalo bi da se završi oko 26. maja 2020. Očekuje se sve manji broj zaraženih, sa trendom pada oko nule.
Na osnovu letimičnog pregleda epidemije SARS, svinjskog gripa i naročito koronavirusa, ovi virusi su se ponašali matematički, po Gausovoj krivoj. Unose se samo podaci za broj zaraženih na dnevnom nivou.
Ne postoji matematički model za predviđanje eventualnog novog talasa mnogo unapred, već to liči na prognozu cunamija – prognoze mogu da počnu neposredno pošto događaj počinje da se odvija. Shodno tome, može da se izda upozorenje da postoji mogućnost (nove) epidemije.
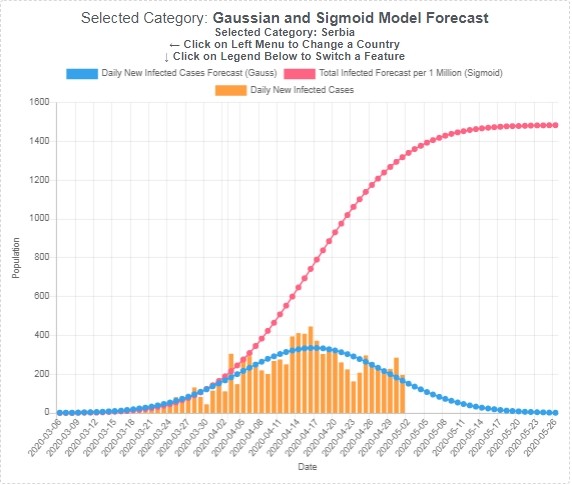 Gausova raspodela nam omogućava da definišemo devet nivoa koji označavaju određene datume za novo upozorenje (pozitivnije ili negativnije od prethodnog), nešto kao u meteorologiji, kada se definišu meteo-alarmi.
Modeliranje epidemije, njenog toka i kraja, kao i mera koje bi trebalo doneti za vreme epidemije je moguć proces. Matematički model se bazira na radu čuvenog nemačkog matematičara i fizičara Johana Karla Fridriha Gausa, najvećeg matematičara od antičkog doba, koji je pojavu raspodele serije događaja primetio i na njoj radio 1794. i 1795. godine. Zbog toga što događaji koji se posmatraju oblikuju zvono, ova raspodela se naziva i normalnom raspodelom ili popularno zvonastom krivom.
Model je dopunio u današnji oblik francuski matematičar Pjer Simon Markus de Laplas, pa se ova raspodela naziva i Gaus–Laplasovom.
Gaus je za zasluge za razvoj matematike našao svoje mesto i na aversu novčanice od 10 nemačkih maraka koja je bila u opticaju od 1898. do 2001. godine. Ova metodologija se koristi u mnogim inženjerskim i ekonomskim disciplinama i marketingu.
Mi ćemo za potrebe kovida 19 umesto reči događaj koristiti pojam epidemiološki dan.
Gausova raspodela nam omogućava da definišemo devet nivoa koji označavaju određene datume za novo upozorenje (pozitivnije ili negativnije od prethodnog), nešto kao u meteorologiji, kada se definišu meteo-alarmi.
Modeliranje epidemije, njenog toka i kraja, kao i mera koje bi trebalo doneti za vreme epidemije je moguć proces. Matematički model se bazira na radu čuvenog nemačkog matematičara i fizičara Johana Karla Fridriha Gausa, najvećeg matematičara od antičkog doba, koji je pojavu raspodele serije događaja primetio i na njoj radio 1794. i 1795. godine. Zbog toga što događaji koji se posmatraju oblikuju zvono, ova raspodela se naziva i normalnom raspodelom ili popularno zvonastom krivom.
Model je dopunio u današnji oblik francuski matematičar Pjer Simon Markus de Laplas, pa se ova raspodela naziva i Gaus–Laplasovom.
Gaus je za zasluge za razvoj matematike našao svoje mesto i na aversu novčanice od 10 nemačkih maraka koja je bila u opticaju od 1898. do 2001. godine. Ova metodologija se koristi u mnogim inženjerskim i ekonomskim disciplinama i marketingu.
Mi ćemo za potrebe kovida 19 umesto reči događaj koristiti pojam epidemiološki dan.
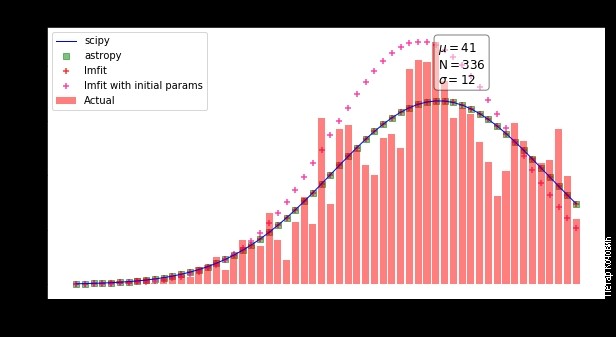 Dakle, na početku je na dnevnom nivou zaraza bila jedan ili nijedan zaraženi. Onda se stvar razbuktala, pa se broj zaraženih povećava. Zatim počinje da se smanjuje. I to smanjenje će biti oko nule, u zavisnosti od par faktora: a) discipline stanovništva da primenjuje mere fizičog rastojanja i b) da se epidemija ne razbukta.
Model se bazira na ulaznim podacima koje sa svet daje Svetska zdravstvena organizacija, a za Srbiju lekarski krizni štab. Ovi podaci se kada je Srbija u pitanju poklapaju, ali to nije slučaj za mnoge sajtove u svetu koji se bave istom tematikom.
Bez obzira na izvor podataka, oni se mogu uvesti pod Gausov model, ali sama kriva i procena kraja epidmije mogu da se razlikuju. Najčešće su razlike male. Kriva se, inače, računa za svaki dan posebno i sa unošenjem novih podataka nema veze sa prethodnim danima.
Gausova kriva kompenzuje manji rast i pad, koji zovemo talas, kao i više talasa. U slučaju da dođe do dramatičnog rasta broja obolelih na dnevnom nivou, onda mora da se pređe na višestruki talasasti model, za čime, za sada, nema potrebe.
Nova epidemija ne može da se predvidi, naročito ako postoji prekid u podacima (recimo tokom leta, pa se nastavi u, recimo, oktobru).
Treba napomenuti da je epidemija koronavirusa i svinjskog gripa bila u korelaciji sa brojem Sunčevih pega i sunčanim ciklusima. Kada je mali broj Sunčevih pega – nema UV-C i IKS zračenja, a ovaj broj tačaka, s obzirom na to da smo izašli iz dna ciklusa, povećava se iz dana u dan, pa će se i epidemija smiriti.
Dakle, na početku je na dnevnom nivou zaraza bila jedan ili nijedan zaraženi. Onda se stvar razbuktala, pa se broj zaraženih povećava. Zatim počinje da se smanjuje. I to smanjenje će biti oko nule, u zavisnosti od par faktora: a) discipline stanovništva da primenjuje mere fizičog rastojanja i b) da se epidemija ne razbukta.
Model se bazira na ulaznim podacima koje sa svet daje Svetska zdravstvena organizacija, a za Srbiju lekarski krizni štab. Ovi podaci se kada je Srbija u pitanju poklapaju, ali to nije slučaj za mnoge sajtove u svetu koji se bave istom tematikom.
Bez obzira na izvor podataka, oni se mogu uvesti pod Gausov model, ali sama kriva i procena kraja epidmije mogu da se razlikuju. Najčešće su razlike male. Kriva se, inače, računa za svaki dan posebno i sa unošenjem novih podataka nema veze sa prethodnim danima.
Gausova kriva kompenzuje manji rast i pad, koji zovemo talas, kao i više talasa. U slučaju da dođe do dramatičnog rasta broja obolelih na dnevnom nivou, onda mora da se pređe na višestruki talasasti model, za čime, za sada, nema potrebe.
Nova epidemija ne može da se predvidi, naročito ako postoji prekid u podacima (recimo tokom leta, pa se nastavi u, recimo, oktobru).
Treba napomenuti da je epidemija koronavirusa i svinjskog gripa bila u korelaciji sa brojem Sunčevih pega i sunčanim ciklusima. Kada je mali broj Sunčevih pega – nema UV-C i IKS zračenja, a ovaj broj tačaka, s obzirom na to da smo izašli iz dna ciklusa, povećava se iz dana u dan, pa će se i epidemija smiriti.

Gausova i Sigmundova kriva

Gausova kriva









Komentari
Budite prvi koji će komentarisati ovu vest!
Ostavite komentar